Acceleration limits of gramophone record grooves

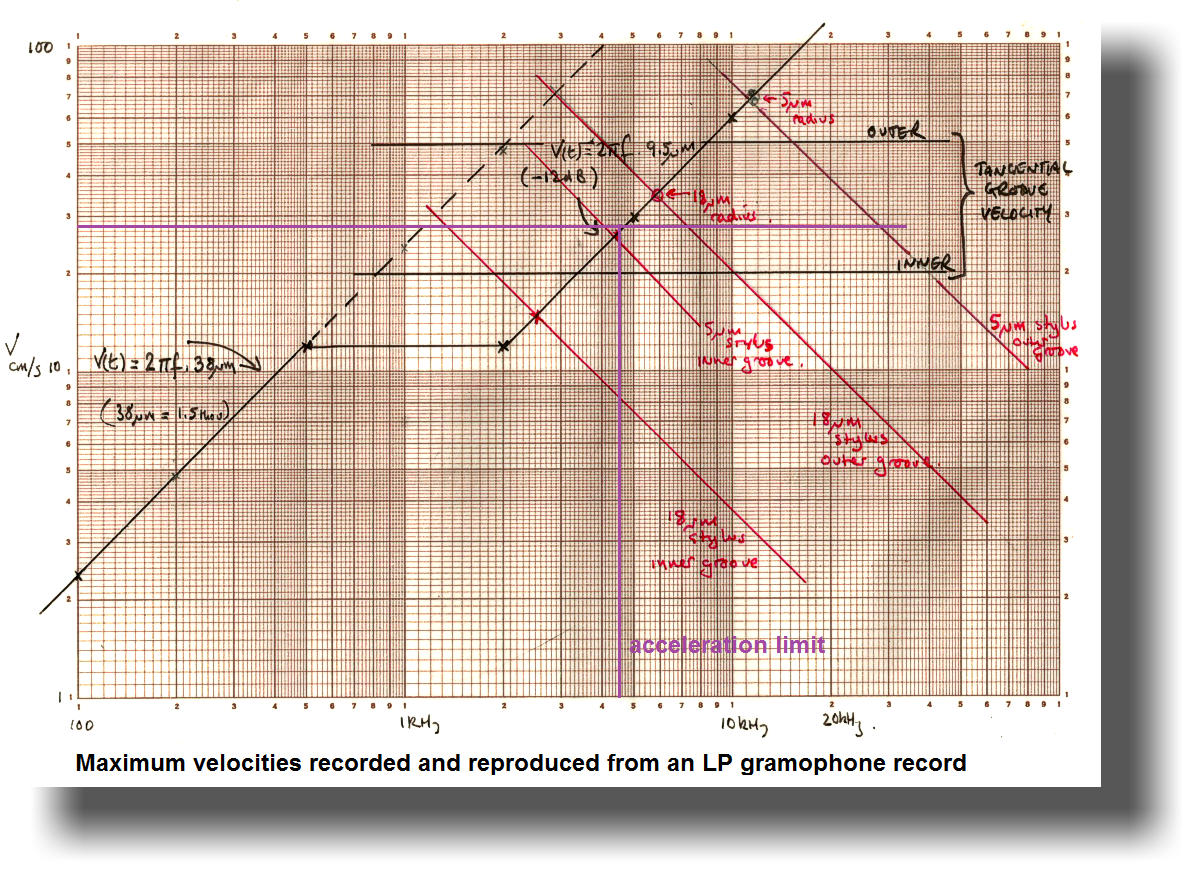
If we look at the main graph above, we can see that the maximum velocity possible (before recording limits are reached) coincides with a frequency just above 8kHz. We can also derive this frequency from the equation for velocity by solving for f, like this,

    v(t) = ω . a . cos ωt

    ω = ^v(t) ⁄ _a

    f = ^ω ⁄ _{2 . π}

Which, if we make a = 9.5μm and v = 0.5m/s, turns out to be equal to 8.3kHz. (Note that cos ωt dissapears early because we are only interested in the maximum point where cos ωt = 1.)

Now the equation for acceleration is the time differential of the velocity equation which is,

    a(t) = (ω)² . a . - sin (ωt)

and, if we substitute the values of 8.3kHz and 9.5μm in this equation it equates to a figure for maximum acceleration of nearly 26,000 m/s² which is equivalent to about 2700 times the acceleration due to gravity.

This is a quite staggering figure. Remember that force = mass . acceleration so acceleration gives us a handle on the forces involved in trying to detach the stylus from the groove which only has the benefit of 1g (gravity itself) holding it there via the tracking downforce¹. With a tracking weight of 1.5 grammes (and thus a downforce of just under 1.5mN), the maximum dynamic mass referred to the stylus point (m) multiplied by the acceleration of that mass needs to balance the force of gravity holding the stylus in the groove so that,

    m × 26000m/s² = 0.0015 × 9.8m/s²

    m = 0.6mg , or half a milligramme!

In principle, these exceptional accelerations are in fact quite possible. The last generation of the Neumann lathes was equipped with power amplifiers which could drive 8 Amps into the cutter drive coils and thereby accelerate the stylus to a limit of 47,500 m/s^{2 Note 2}.

But, as the graph above clearly shows, this acceleration results in a groove radius which even the best styli cannot negotiate on inner grooves and which conical styli cannot negotiate at any point on the disc. In addition, the required dynamic mass of the cartridge armature referred to the stylus point (as calculated above) would be very difficult to accomplish in a practical design and this would mean that the stylus would fail to remain in contact with the groove.

The result of all this exceptionally clever engineering on the consumer is thereby not her delight at "razor sharp transients". Rather, assuming the cartridge does not jump out of the groove - it will lead to disappointment due to the most typical practical manifestation of mistracking due to acceleration-limiting which appears on the sibilant energy associated with the sung "s". A closely miked recording of a singer will often contain very substantial HF content which might record and reproduce well on studio equipment, but once transferred to acetate results in a nasty mushy "shhh" sound where the original recording has a pure "sss" sound.

This phenomenon presents the mastering engineer with a tricky problem. What is needed is a progressive, dynamic tone control which can be made to act so as to "duck" HF frequencies only when the treble energy reaches the particular, troublesome threshold. Such a device is known as a de-esser. Most disc mastering involves some sort of processing of this sort (for example, the Neumann HK66 in the VG66 rack), and Neumann even invented a dedicated, calibrated acceleration limiter for their later lathes (the BSB-74 unit). Both these units act on the same principle as a de-esser.

The BSB-74 acceleration limiter was calibrated to a current limit of 1.4 Amps in the band above 4kHz thereby limiting all accelerations to 8150m/s². This limit, in terms of frequency-limit and in terms of velocity, is indicated on the graph by the purple lines.

With the calibrated acceleration limit of 8150m/s² (830g), maximum groove modulation is limited to a frequency of 4.6kHz and maximum velocity to a limit of 28cm/s. The graph reveals that Neumann made the perfect choice in chosing this limit because it guarantees that a 5μm effective radius stylus can negotiate any groove so limited at all recorded radii.

In terms of tracking weights to keep the stylus sitting in the groove. If we take a reasonably practical figure of 1.25mg as the dynamic mass of the cartridge armature referred to the stylus point, we can calculate that the required tracking weight to counteract the acceleration upon this mass will be,

    (1.25 × 10^-6) kg × 8150 m/s² / 9.8 m/s²

    = 1 gramme

a figure which we know will not deform the PVC too far beyond its elastic limits (1.5g being the generally accepted upper limit of playing weight to maintian maximum record life.)^{3, 4}

Is this the origin of the analogue magic?

There is all manner of anecdotal evidence which suggests that the use of acceleration limiters (or de-essers) accounts for the difference in sound-quality between LP and CD releases of the same music; listeners apparently prefering the HF limited version.

Certainly it's possible to argue that the significant limitations on velocity and acceleration imposed by the physical medium of the vinyl record account for the commonly cited "warmth" of the medium. Uncompressed PCM audio files (even at standard sampling-rate) do not impose any restriction on high-frequencies. Thus, a gramophone record with the same performance as a CD would support a maximum groove velocity of 525cm/s. And a 96kHz uncompressed audio file has the equivalent acceleration limit of 3.5 million gravities, a figure which would mean a typical cartridge would need to a playing weight of ½ kg to keep it in the groove!

¹ When the lateral force on the stylus is equal to the force of gravity holding it in the groove, the resultant force is perpendicular to the 45° inclined slope of the groove wall. This is the last stable point. Any further increase in lateral force will tend to drive the stylus from the groove against friction.

³Stereo Gramophone Pickups. S. Kelly. Wireless World . December 1969

⁴ If we take the practical upper acceleration-limit to be 1000g or 10,000 m/s² and g = 10 m/s², we can forge the simple rule of thumb that the dynamic mass of the cartridge armature referred to the stylus point must be ¹⁄₁₀₀₀ th of the playing weight.

Links

For all support issues, go here.

For Pspatial Audio sales, email: sales@pspatialaudio.com